Real Numbers, Units and Finalness
As you might have seen from our change log, I've been recently working on a bunch of new core features for our NKSP real-time instrument script engine, with the goal to make instrument scripting more intuitive and less error prone, especially from a musician's point of view.
The changes are quite substantial, so here is a more detailed description of what's new, how to use those new features, what's the motivation behind them, and also a discourse about some of the associated language design (and implementation) aspects.
64-Bit Integers
First of all, integers, i.e. integer number literals (as e.g. 4294967295), integer
variables (like declare $foo := 4294967295), or
integer array variables (like declare %bar[3] := ( 1, 2, 3 ) ),
and all their arithmetics like
($foo + 1024) / 24 and all built-in functions (as e.g.
min()), are now all 64 bit with NKSP.
I hear your "Yaaawn" at this point. You might be surprised though about the amount of
diff involved
and how often people stumbled over undesired 32-bit truncation with their
scripts before. So that change alone reduced error-proneness tremendously.
But let's get on.
Real Numbers
You are finally no longer limited to integer math with NKSP.
You can now also use floating point arithmetics which will make calculations,
that is mathematical formulas in your scripts much easier than before.
Sounds a bit more interesting, doesn't it?
Variables
We call those floating point numbers
real numbers
from now on and you can
write them like you probably already expected; in simple dotted notation like
2.98. Likewise there are new variable types for real numbers as well.
The syntax to declare a real number variable is:
declare ~real-variable-name := initial-value
Like e.g.:
declare ~foo := 3.14159265
So it looks pretty much the same as with integer variables, just that you use "~" as prefix in front of the variable name instead of "$" that you would use for integer variables and the values must always contain a dot so that the parser can distinguish them clearly from integer numbers. Moreover there is now also a real number array variable type which you can declare like this:
declare ?real-array-variable-name[amount-of-elements] := ( initial-values )
Like e.g.:
declare ?foo[4] := ( 0.1, 2.0, 46.238, 104.97 )
Once again, the only differences to integer array variables are that you use
"?" as prefix in front of the array variable name instead of "%" that you
would use for integer array variables, and that you must always use a
dot for each value being assigned.
And as with integer variables, if you omit to assign initial value(s) for
your real number variables or real array variables then they are automatically
initialized with zero value(s) (that is 0.0 actually).
Type Casting
Like KSP we are (currently) quite strict about your obligation to distinguish clearly between integer numbers and real numbers with NKSP. That means blindly mixing integers and real numbers e.g. in formulas, will currently cause a parser error like in this example:
~foo := (~bar + 1.9) / 24 { WRONG! }
In this example you would simply use 24.0 instead of 24 to
fix the parser error:
~foo := (~bar + 1.9) / 24.0 { correct }
That's because, when you are mixing integer numbers and real numbers in mathematical operations, like the division in the latter example, what was your intended data type that you expected of the result of that division; a real number or an integer result? Because it would not only mean a different data type, it might certainly also mean a completely different result value accordingly.
That does not mean you were not allowed to mix real numbers with integers, it is just
that you have to make your point clear to the parser what your intention is. For that
purpose there are now 2 new built-in functions int_to_real() and
real_to_int() which you may use for required type casts (data type conversions).
So let's say you have a mathematical formula where you want to mix that formula with
a real number variable and an integer variable, then you might e.g. type cast the
integer variable like this:
~bla := ~foo / int_to_real($bar)
And since this is a very common thing to do, we also have 2 short-hand forms of these
2 built-in functions in NKSP which are simply real() and int():
~bla := ~foo / real($bar) { same as above, just shorter }
real() and int() only exist in
NKSP. They don't exist with KSP.
Built-in Functions
What about real numbers and existing built-in functions? When you check our latest reference documentation of NKSP built-in functions, you will notice that most of them accept now both, integers and real numbers as arguments to their function calls. You should be aware though that the precise acceptance of data types and the resulting behaviour change, varies between the individual built-in functions, which is due to the difference in purpose of all those numerous built-in functions.
For instance the data type of the result returned by min() and max()
function calls depends now on the data type being passed to those functions. That is
if you pass real numbers to those 2 functions then you'll get a real number as result;
if you pass integers instead then you'll get an integer as result instead.
Then there are functions, like e.g. the new math functions sin(), cos(),
tan(), sqrt(), which only accept real numbers as arguments (and
always return a real number as result). Trying to pass integers will cause a parser error,
because those particular functions are not really useful on integers at all.
Likewise the previously already existing functions fade_in() and fade_out()
accept now both integers and real numbers for their 2nd argument (duration-us),
but do not allow real numbers for their 1st argument (note-id), because for
a duration real numbers make sense, whereas for a note-id
real numbers would not make any sense and such an attempt is usually a result of some
programming error, hence you will get a parser error when trying to pass a real number
to the 1st argument of those 2 built-in functions.
There might also be differences how built-in functions handle mixed usage of integers
and real numbers as arguments, simultaniously for the same function call that is.
For instance
the min() and max() functions are very permissive and allow you to mix
an integer argument with a real number argument. In such mixed cases those 2 functions
will simply handle the integer argument as if it was a real number and hence the
result's data type would be a real number. So this would be Ok:
min(0.3, 300) { OK for this function: mixed real and integer arguments }
Yet other functions,
like the search()
function, are very strict regarding data type. So if you are passing an integer array as 1st argument to
the search() function then it only accepts an integer (scalar) as
2nd argument, and likewise if you are passing a real number array as 1st argument
then it only accepts a real number (scalar) as 2nd argument. Attempts passing
different types, or in a different way to that function, will cause a parser error.
Comparing for Equalness
If you are also writing KSP scripts, then you probably already knew most of the things that I described above about real numbers. But here comes an important difference that we have when dealing with real numbers in NKSP: real number value comparison for equalness and unequalness.
In our automated NKSP core language test cases you find an example that looks like this (slightly changed here for simplicity):
- on init
- declare ~a := 0.165
- declare ~b := 0.185
- declare ~x := 0.1
- declare ~y := 0.25
- if (~a + ~b = ~x + ~y)
- message("Test succeeded")
- else
- message("Test failed")
- end if
- end on
When you add the values of those variables from this example in your head, you will see that the actual
test in that example theoretically boils down to comparing if (0.35 = 0.35).
Hence this test should always succeed. At least
that's what one would expect if one would do the calculations above manually by humans
in the real world.
In practice though, when this script is executed on a computer, the numbers on both sides would
slightly deviate from 0.35. These differences to the expected value are
actually extremely little, that is very tiny fractions of several digits behind the decimal point,
but the final consequence would still be nevertheless different values on both sides and this test "would" hence fail.
These small errors are due to the technical way
floating point numbers are encoded
on any modern CPU which causes small calculation errors with these summations for instance.
Due to that very well known circumstance of floating point arithmetics on
CPUs, it is commonly discouraged with system programming languages like C/C++
to directly compare floating point numbers for equalness, nor for unequalness for that exact reason.
However the use case for the NKSP language is completely different from
system level programming languages like C/C++. We don't need to be so
conservative in many aspects those languages need to be. The musical context of
NKSP simply has different requirements. Simplicity and high level
handling is more important for NKSP than revealing bit by bit
of the actual CPU registers bare-bone directly to users of instrument scripts.
So I decided to implement
real number equal (= operator) and unequal comparison
(# operator) to automatically take the expected floating
point tolerances of the underlying CPU into account.
So in short: the test case example above does not fail with our NKSP implementation!
That does not mean you can simply switch off your head when doing
real number arithmetics and subsequent comparisons of those calculations.
Because with every calculation you do, the total amount of calculation
error (caused by the utilized floating point processing hardware) increases,
so after a certain amount of subsequent calculations
our equal/unequal comparisons would fail as well after a certain point.
But most of the time you will have formulas which end up with a very
limited amount of floating point calculations before you eventually
do your comparisons, so in most cases you should just be fine. But keep
this issue in mind when doing e.g. numeric (large amount of subsequent)
calculations e.g. in while loops.
What about the other comparison operators like <,
>, <=, >=? Well,
those other comparison operators all behave like with system level
programming languages. So these comparison operators currently
do not take the mentioned floating point tolerances into
account and hence they behave differently than the =
and # operators with NKSP.
The idea was that those other
comparison operators are typically used for what mathematicians
call "transitivity". So they are used e.g. for sorting tasks
where there should always be a clear determinism of the
comparison results, and where execution speed is an issue as well.
Because the truth is also that our floating point tolerance
aware "equal" / "unequal" comparisons come with the price of
requiring execution of additional calculations on the underlying CPU.
Yes, we could implement support for real numbers as so called algebraic system, which would accomplish that real number calculations would always exactly result as you would expect them to do from traditional mathematics, like certain mathematical software applications use to do it (e.g. Maple). However to achieve that we could no longer utilize hardware acceleration of the CPU's floating point unit, because it is limited to floating point values of fixed precision (e.g. either 32 bit and/or 64 bit). Hence we would need to execute a huge amount of instructions on the CPU instead for every single real number calculation in scripts, so there would be a severe performance penalty.
And no, we actually cannot do that in NKSP at all, because this kind of complex real number implementation would require memory allocations at runtime, which in turn would violate a key feature of NKSP scripting: its guaranteed real-time stability and runtime determinism.
Standard Measuring Units
If you are coming from KSP then you are eventually going to think next "WTF? What is this all about?". But hang with me, no matter how often you wrote instrument scripts before, you will most certainly regularly come into a situation like described next and we have a convenient fix for that.
Unit Literals
Let's consider you wanted to pause your script at a certain point for let's say
1 second. Ok, you remember from the back of your head that you need to use the
built-in wait() function for that, but which value do you need to
pass exactly to achieve that 1 second break?
Would it be wait(1000)
or probably wait(1000000)? Of course now you reach out for the
reference documentation at this point and eventually find out that it
would actually be wait(1000000). Not very intuitive. And
the large amount of zeros required does not help to make your code necessarily
more readable either, right?
So what about actually writing what we had in mind at first place:
wait(1s)
It couldn't be much clearer.
Or you want a break of 23 milliseconds instead? Then let's just write that!
wait(23ms)
Now let's consider another example: Say you wanted to reduce volume of some voices by 3.5 decibel.
You remember that was something like change_vol(note, volume),
but what would volume be exactly? Digging out the docs yet again you
find out the correct call was change_vol($EVENT_ID, -3500).
We can do better than that:
change_vol($EVENT_ID, -3.5dB)
You rather want a slight volume increase by just 56 milli dB instead?
change_vol($EVENT_ID, +56mdB)
Or let's lower the tuning of a note by -24 Cents:
change_tune($EVENT_ID, -24c)
I'm sure you got the point. We are naturally using standard measuring units in our daily life without noticing their importance, but they actually help us a lot to give some otherwise purely abstract numbers an intuitive meaning to us. Hence it just made sense to add measuring units as core feature of the NKSP language, their built-in functions, variables and whatever you do with them.
Calculating with Units
Having said that, these examples above were just meant as warm up appetizer. Of course you can do much more with this feature than just passing them literally to some built-in function call as we did above so far. You can assign them to variables, too, like:
declare ~pitchLfoFrequency := 1.2kHz
You can use them in combinations with integers or real numbers, and of course you can do all mathematical calculations and comparisons that you would naturally be able to do in real life. For instance the following example
- on init
- declare $a := 1s
- declare $b := 12ms
- declare $result := $a - $b
- message("Result of calculation is " & $result)
- end on
would print the text "Result of calculation is 988ms" to the terminal
(notice that $a and $b actually used different units here).
Or the following example
- on init
- declare ~a := 2.0mdB
- declare ~b := 3.2mdB
- message( 4.0 * ( ~a + ~b ) / 2.0 + 0.1mdB )
- end on
would print the text "10.5mdB" to the terminal.
Or let's make this little value comparison check:
- on init
- declare ~foo := 999ms
- declare ~bar := 1s
- if (~foo < ~bar)
- message("Test succeeded")
- else
- message("Test failed")
- end fi
- end on
which will succeed of course
(notice again that ~foo and ~bar used different units here as well).
So as you can see the units are not just eye candy for your code, they
are actually interpreted actively by the script engine appropriately such that all your
calculations, comparisons and function calls behave as
you would expect them to do from your real-life experience.
Unit Components
In the examples above you might have noticed that the units' components were shown in different colors. That's not a glitch of the website, that's intentional and in fact NKSP code on this website is in general, automatically displayed in the same way as with e.g. Gigedit's instrument script editor. So what's the deal?
If you take the value 6.8mdB as an example, you have in front
the numeric component = 6.8 of course, followed
by the metric prefix = md for
"milli deci" (which is always simply some kind of multiplication factor)
and finally the fundamental unit type = B for "Bel" (which actually gives the number its final meaning).
So here's where language design comes into play. From language point of view both
the numeric component and the optional metric prefix
are runtime features which may change at any time,
whereas the optional unit type is always
a constant, "sticky", parse-time feature that you may never change at runtime.
That means if you define a variable like e.g. declare $foo := 1s
that variable $foo is now firmly tied to the unit type "seconds" for your entire script.
You may change the variable's numeric component and metric prefix later on at any time like e.g.
$foo := 8ms, but you must not change the variable ever to a different
unit type later on like $foo := 8Hz. Trying to switch
the variable to a different unit type that way will cause a parser error.
Changing the fundamental unit type of a variable is not allowed, because it
would change the semantical meaning of the variable.
So getting back and proceed with an early example, this code would be fine:
- on note
- declare ~reduction := -3.5dB { correct unit type }
- change_vol($EVENT_ID, ~reduction)
- end note
That's Ok because the built-in function change_vol()
optionally accepts the unit B for its 2nd argument.
Whereas the following would immediately raise a parser error:
- on note
- declare ~reduction := -3.5kHz { WRONG unit type for change_vol() call! }
- change_vol($EVENT_ID, ~reduction)
- end note
That's because using the unit type Hertz for changing volume with the
built-in function change_vol() does not make any sense,
that built-in function expects a unit type suitable for volume changes,
not a unit type for frequencies, and hence it is clearly a
programming mistake. So getting this error in
practice, you may have simply picked a wrong variable by accident for
a certain function call for instance and the parser will immediately
point you on that undesired circumstance.
As another example, you may now also use units with the built-in random number
generating function like e.g. random(100Hz, 5kHz). The function
would then return an arbitrary value between 100Hz and 5kHz
each time you call it that way, so that makes sense. But trying e.g. random(100Hz, 5s)
would not make any sense and consequently you would immediately get a parser
error that you are attempting to pass two different unit types to the random() function,
which is not accepted by this particular built-in function.
And these kinds of parse-time errors are always detected,
no matter whether you are literally passing constant
values like in the simple example here, but also through every other means like
variables and complex mathematical expressions.
The following tables list the unit types and metric prefixes currently supported by NKSP.
| Unit Type | Description | Purpose |
|---|---|---|
s |
short for "seconds" | May be used for time durations. |
Hz |
short for "Hertz" | May be used for frequencies. |
B |
short for "Bel" | May be used for volume changes and other kinds of relative changes (e.g. depth of envelope generators). |
| Metric Prefix | Description | Equivalent Factor |
|---|---|---|
u |
short for "micro" | 10-6 = 0.000001 |
m |
short for "milli" | 10-3 = 0.001 |
c |
short for "centi" | 10-2 = 0.01 |
d |
short for "deci" | 10-1 = 0.1 |
da |
short for "deca" | 101 = 10 |
h |
short for "hecto" | 102 = 100 |
k |
short for "kilo" | 103 = 1000 |
Of course there are much more standard unit types and metric prefixes than those, but currently we only support those listed above. Simply because I found these listed ones to be actually useful for instrument scripts.
change_tune($EVENT_ID, -24c), you might have noticed
already from the markup color here, that this is actually not handled as a unit
type by the NKSP language and that's why it is not listed as
a unit type in the table above. So tuning changes in "Cents" is actually just a value
with metric prefix "centi" and without any unit type, since tuning changes
in "Cents" is really just a relative multiplication factor for changing the pitch of
a note depending on the current base frequency of the note.This might look a bit odd to you, it is semantically however absolutely correct to handle tuning changes in "Cents" that way by the language. You can still also use expressions like "milli Cents", e.g.:
change_tune($EVENT_ID, +324mc), which is also
valid since we (currently) allow a combination of up to 2 metric prefixes with NKSP.The obvious advantage of not making "Cents" a dedicated unit type is that we can just use the character "c" in scripts both for tuning changes, as well as for conventional "centi" metric usage like
1cs ("one centi second").
The downside of this design decision (that is "Cents" being defined as metric prefix) on the other hand
means that we loose the previously described parse-time stickyness feature that we
would have with "real" unit types, and hence also loose some of the described
error detection mechanisms that we have with "real" unit types at parse time.In practice that means: you need to be a bit more cautious when doing calculations with tuning values in "Cents" compared to other tasks like volume changes, because with every calculation you do in your scripts, you might accidentally drop the "Cents" from your unit, which eventually will cause e.g. the
change_tune() function to
behave completely differently (since a value without any metric prefix
will then be interpreted by change_tune() to be a value in "milli cents",
exactly like this function did before introduction of units feature in NKSP).
Unit Conversion
Even though you are not allowed to change the unit type of a variable itself by assignment at runtime, that does not mean there was no way to get rid of units or that you were unable to convert values from one unit type to a different unit type. You can do that very easily actually with NKSP, exactly as you learned in school; i.e. by multiplications and divisions.
Let's say you have a variable $someFrequency that you
use for controlling some LFO's frequency by script, and for some reason you really
want to use the same value of that variable (for what reason ever)
to change some volume with change_vol(), then all you have
to do is dividing the existing unit type away, and multiplying it
with the new unit type:
- on note
- declare $someFrequency := 100Hz
- change_vol($EVENT_ID, $someFrequency / 1Hz * 1mdB)
- end note
Which would convert the variable's original value 100Hz
to 100mdB before passing it to the change_vol()
function. So this actually did 3 things:
- the divsion (by
/ 1Hz) dropped the old unit type (Hertz), - the multiplication (by
* 1mdB) added the new unit type (Bel) - and that multiplication also changed the metric prefix (to milli deci) before the result is finally passed to the
change_vol()function.
And since change_vol() would now receive the value
in correct unit type, this overall solution is hence legal and accepted by the parser without any complaint.
And this type of unit conversion does not break any parse-time determinism
and error detection features either, since it is not touching the variable's
unit type directly (only the temporary value eventually being passed to the change_vol() function here),
and so the result of the unit conversion expressions above
can always reliably be evaluated by the parser at parse-time.
100Hz * 1B, nor
with the same unit type like e.g. 4s * 8s. That's because we don't have
any practical usage for e.g. "square seconds" or other kinds of mixed unit types
in instrument scripts.
So trying to create a number or variable with more than one unit type will always
raise a parser error. So keep that in mind and use common sense when writing
calculations with units. And like always: the parser will always point you on
misusage immediately.
Array Variables
And as we are at limitations regarding units: Currently unit types are not accepted for array variables yet. Metric prefixes are allowed though!
- declare %foo[4] := ( 800, 1m, 14c, 43) { OK - metric prefixes, but no unit types }
- declare %bar[4] := ( 800s, 1ms, 14kHz, 43mdB) { WRONG - unit types not allowed for arrays yet }
Main reason for that current limitation is that unlike with scalar variables,
accessing array variables at runtime with an index by yet another (runtime changeable)
variable might break the previously described parse-time determinism of unit types.
That means if we just take the array variable %bar[] declared above
and would access it in our scripts with another variable like:
%bar[$someVar]
then what would that unit type of that array access be? Notice that the array variable
%bar[] was initialized with 3 different unit types for its individual elements.
So the unit type of the array access would obviously depend on the precise
value of variable $someVar, which most probably will change at runtime and
hence the compiler would not know at parse-time yet.
Finalness
Here comes another new core language feature of NKSP that you certainly don't know from KSP (as it does not exist there), and which definitely requires an elaborate explanation of what it is about: "finalizing" some value.
Default Relativity
When changing synthesis parameters, these are commonly relative changes, depending
on other modulation sources. For instance let's say you are using change_vol()
in your script to change the volume of voices of a note, then the actual, final volume
value being applied to the voices is not just the value that you passed to change_vol(),
but rather a combination of that value and values of other modulation sources of volume
like a constant gain setting stored with the instrument patch, as well as a continuously
changing value coming from an amplitude LFO
that you might be using in your instrument patch, and you might most certainly also use
an amplitude envelope generator which will also have its impact on the final volume of course.
All these individual volume values are multiplied with each other in real-time by the sampler's engine core
to eventually calculate the actual, final volume to be applied to the voices, like illustrated in the following
schematic figure.
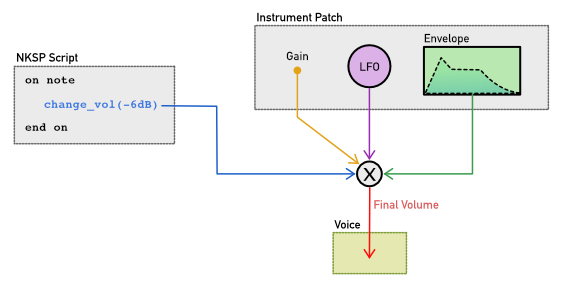
This relative handling of synthesis parameters is a good thing, because multiple
modulation sources combined make up a vivid sound. However there are situations where this
combined behaviour for synthesis parameters is not what you want. Sometimes you want to be
able to just say in your script e.g. "Make the volume of those voices exactly -6dB. Period. I mean it!".
And that's exactly what the newly introduced "final" operator ! does.
Final Operator
- on note
- declare $volume := -6dB
- change_vol($EVENT_ID, !$volume) { '!' makes value read from variable $volume to become 'final' }
- end note
By prepending an exclamation mark ! in front of an expression as shown in the code above,
you mark that value of that expression to be "final",
wich means the value will bypass the values of all other modulation sources, so the
sampler will ignore all other modulation sources that may exist, and
will simply use your script's value exclusively for that synthesis parameter,
as illustrated in the following figure:
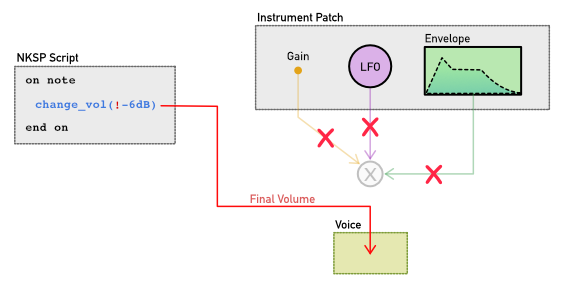
You can of course revert back at any time to let the sampler process that synthesis parameter
relatively again by calling change_vol() and just passing
a value for volume without "finalness" (i.e. without ! operator) this time.
In the previous code example, the "finalness" was applied to the temporary value
being passed to the change_vol() function, it did not change
the information stored in variable $volume at all though. So this is different
from:
- on note
- declare $volume := !-6dB { store 'finalness' directly to variable $volume }
- change_vol($EVENT_ID, $volume)
- end note
In the latter code example the actual "finalness" is stored directly now
to the $volume variable instead. Both approaches
make sense depending on the actual use case. For instance if you only
need "finalness" in rare situations, then you might use the prior
solution by using the "final" operator just with the respective function call,
whereas in use cases where you would always apply the
$volume "finally" and probably need to pass it to several
change_vol() function calls at several places in your script,
then you might store the "finalness" information directly to the variable instead.
! "final" operator is resolved in
expressions.
Mixed Finalness
Like with the other new language features described previously above, we also have some potential ambiguities that we need to deal with when applying "finalness". For instance consider this code:
- on note
- declare $volume := !-6dB { store 'finalness' directly to variable $volume }
- change_vol($EVENT_ID, $volume + 2dB) { raises parser warning here ! }
- end note
Should the resulting, expected volume change of -4dB be applied as
"final" value or as relative value instead?
Because the problem here is that !-6dB obviously means "final",
whereas + 2dB is actually a relative value to be added.
In the current version of the sampler the value to be applied in this case would be "final", so you will not get a parser error, however you will get a parser warning to make you aware about this ambiguity. So to fix the example above, that is to to get rid of that parser warning, you can simply add an exclamation mark in front of the other number as well like:
- on note
- declare $volume := !-6dB { store 'finalness' directly to variable $volume }
- change_vol($EVENT_ID, $volume + !2dB) { '!' fixes parser warning }
- end note
Also built-in functions will behave similarly as described above. Certain built-in functions accept finalness for all of their arguments, some functions accept finalness for only certain arguments and some functions won't accept finalness at all. Like with the other new core language features always use common sense and quickly think about whether it would make sense if a certain function would accept finalness for its argument(s). Most of the time your guess will be right, and if not, then the parser will tell you immediately with either an error or warning, and the NKSP built-in functions reference will help you out with details in such rare cases where things might not be clear to you immediately.
Implied Finalness
Here comes the point where the feature circle of this article closes: the unit type "Bel" used in the examples for the "final" operator above is somewhat special, since the unit type "Bel" is in general used for relative quantities like i.e. volume changes. Tuning changes (i.e. in "Cents") are also relative quantities.
However other unit types like "seconds" or "Hertz" are absolute
quantities. That means if you are using unit types "Hertz" or "seconds" in your scripts, then their
values are automatically applied as implied "final" values, as if you were using the !
operator for them in your code. The parser will raise a parser warning though to point you on that
circumstance.
The following table outlines this issue for the currently supported unit types.
| Unit Type | Relative | Final | Reason |
|---|---|---|---|
| None | Yes, by default. | Yes, if ! is used. |
If no unit type is used (which includes if only a metric prefix is used like e.g. change_tune($EVENT_ID, -23c)) then such values can be used both for relative, as well as for 'final' changes. |
s |
No, never. | Yes, always. | This unit type is naturally for absolute values only, which implies its value to be always 'final'. |
Hz |
No, never. | Yes, always. | This unit type is naturally for absolute values only, which implies its value to be always 'final'. |
B |
Yes, by default. | Yes, if ! is used. |
This unit type is naturally for relative changes. So this unit type can be used both for relative, as well as for 'final' changes. |
! operator.
Array Variables
As with unit types, the same current restriction applies to "finalness" in conjunction with array variables at the moment: you may currently not apply "finalness" to the elements of array variables yet.
declare %foo[3] := ( !-6dB, -8dB, !2dB ) { WRONG - finalness not allowed for arrays (yet) ! }
The reason is also exactly the same, because finalness is a parse-time required information
and an array access by using yet another variable like e.g. %foo[$someVar] might
break that parse-time awareness of "finalness" for the compiler.
Backward Compatibility
You might be asking, what do all those new features mean to your existing instrument scripts, do they break your old scripts?
The clear and short answer is: No, of course they do not break your existing scripts!
Our goal was always to preserve constant behaviour for existing sounds, so that even ancient sound files in GigaSampler v1 format still would sound exactly as you heard them originally for the 1st time many, many years ago (probably with GigaSampler at that time). And that means the same policy applies to instrument scripts as well of course.
You can also arbitrarily mix your existing instrument scripts by just partly using the new features described in this article at some sections of your scripts, while at the same time preserving your old code at other code sections. So these features are designed that they won't break anything existing, and that they always collaborate correctly in an arbitrary, mixed way with old NKSP code.
Status Quo
That's it! For now ...
This is the current development state regarding these new NKSP core language features. It might not be the final word though. I am aware certain aspects that I decided can be argued about (or maybe even entire features). And that's actually one of the reasons why I decided to write this (even for my habits) quite long and detailed article, which also explained the reasons for individual language design decisions that I took.
You can however share your thoughts and arguments about these new features with us on the mailing list of course!
